this information on this page is still in draft form
Magnetism
Introduction
The ancient Greeks knew that a type of rock with magnetic properties known as lodestone or magnetite attracted iron. The compass, an important device for navigation, has a suspended magnet which aligns parallel to the magnetic field produced by the Earth and as a result points to the North pole The compass was documented as early as 1040. The Ching Tsung Yao describes how iron can be magnetised by heating and quenching in water. It is known that the Vikings used Lodestone to navigate. By the end of the twelfth century, Europeans were using this simple compass to aid navigation. A steel needle stroked with such a "lodestone" became "magnetic" as well.
In 1600, William Gilbert (also known as Gilberd) of Colchester proposed an explanation in his work De Magnet for the operation of the compass and that The Earth itself was a giant magnet, with its magnetic poles some distance away from its geographic ones (i.e. near the points defining the axis around which the Earth turns). He made an experimental model of the earth by creating a Lodestone sphere.
Properties of Magnets

William Gilbert also experimented on bar magnets and found the following properties:
A magnet will always have two poles which we call arbitrarily North and South. I the magnet is broken in two this will create two new magnets with North (N) and South (S) poles. If a bar magnet is broken in two, at the fracture new north and south poles are formed at the point of fracture.
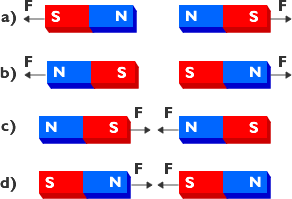
- Like poles repel each other. If a N pole is brought close to the N pole of a second magnet a repulsive force will be felt. Similarly if a S pole is brought close to the S pole of another magnet, the two magnets will repel each other.
- Unlike poles attract and will stick together.
- Magnets attract iron rich materials and like poles and the repulsion between like poles can be reduced if a strip of iron is placed between them.
The Domain Theory of Magnetism
How can we explain these intriguing properties? The domain theory states that inside a magnet there are small regions in which the magnetic direction of all the atoms are aligned in the same directions. These regions are known as domains.
Within a domain, the aligment of the magnetic direction is the same. In the next domain it may be in a completely different direction. On average over the many domains in the magnet there there is no preferential direction for the magnetic force. However, using an external magnetic field from another magnet say, the direction of the magnetic direction in each domain can be made to align with the magnetic field the net magnetic field can be increased.
Why do Magnetic Domains Form?
Consider a bar magnet which has been been magnetised such that the entire magnet forms a single magnetic domain. Surface charges will appear at either end of the crystal. Associated with the surface charges is a secondary magnetic field called the demagnetising field which acts to reduce the magnetic field. The energy of the surface charges is called the magnetostatic energy.
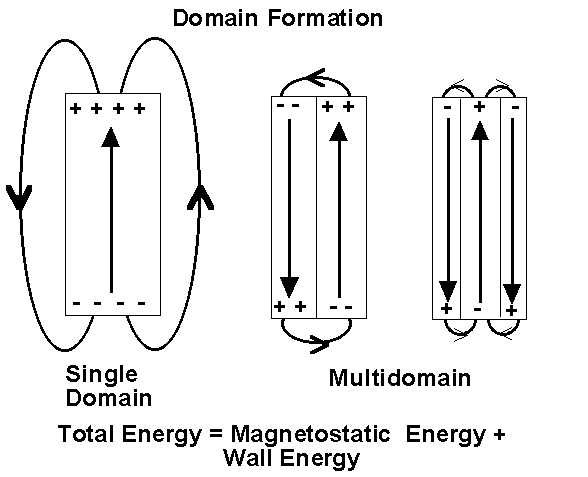
The magnetostatic energy can be reduced if the crystal forms a second domain, magnetised in the opposite direction. In this way, the separation of positive and negative surface charges are reduced decreasing the spatial extent of the demagnetising field.
Naturally, one might ask, if the magnetostatic energy is reduced by the formation of domains, can they carry on forming indefinitely? To which the answer is no. The reason being that energy is required to produce and maintain the region of transition from one domain to another, the domain wall. Equilibrium will be reached when the magnetostatic energy is equal to the energy required to maintain the domain walls. However, domains are much larger than the individual molecules within the magnet.
There are only 4 ferromagnetic elements at room temperature. Of these, iron (Fe), nickel (Ni), and cobalt (Co) are shown above. The fourth is gadolinium (Gd).
The pictures below show the formation made visible with the use of magnetic colloidal suspensions which concentrate along the domain boundaries. The domain boundaries can be imaged by polarized light, and also with the use of electron diffraction. Observation of domain boundary movement under the influence of applied magnetic fields has aided in the development of theoretical treatments. It has been demonstrated that the formation of domains minimizes the magnetic contribution to the free energy.

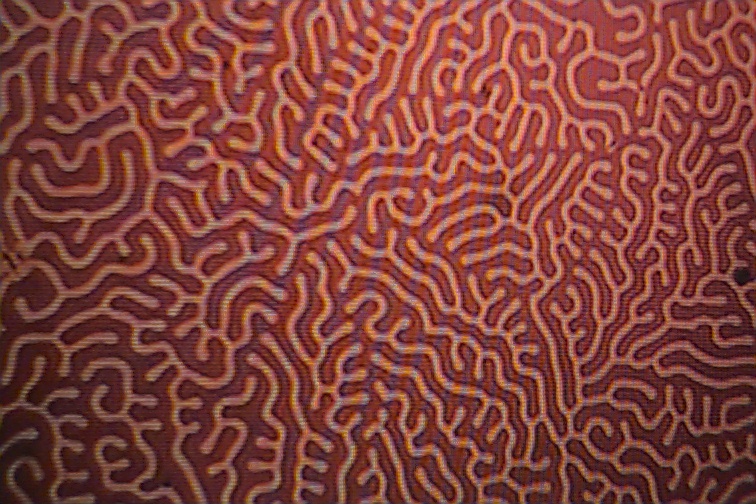

If a magnetic field is applied to the crystal, the domains that align with the magentic field will grow as the expense of the domains that are pointing in other directions.
Atomic Theory of Magnetism
We are familiar with the model of the atom with a nucleus that contains the protons and neutrons and electron orbit the nucleus. Within the atom, the electrons behave as if they are magnets. Electrons, protons and neutrons all have a magnetic dipole moments however the magnetic moment of an electron is the most significant. In fact it is conveniently assigned a unit called the Bohr magneton, which is equal to the magnetic dipole moment of an electron. (μB = m/2e = 9.274 x 10-24 J T-1)
In addition to the magnetic dipole moment of the electrons, the fact that the electrons orbit around the nucleus give rise to a second magnetic field produced by the moving charge around the nucleus.
The Magnetic Field
Magnetic field strength is given the symbol H with the unit Tesla
Magnetic flux density is given the symbol B and has the unit (W m-2)
To measure the magnetic field caused by a current the Biot Savart law is used
The magnetic field is a vector field which means that it has a magnitude and direction for each point in space. The strength and direction of the magnetic field at any point is defined in terms of the force on a moving charged particle such as an electron. The force created the magnetic field comes from the Lorentz equation without the electric field. by measuring the force on a unit test charge. The magnetude and direction come from the Lorentz force equation.
F = q(v x B)
Since we are dealing with a cross-product, the direction of the force is a direction perpendicular to the plane of v and B. and the magnitude of the force is then F = q v B sin θ
where theta is the angle between B and v
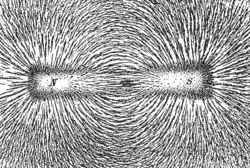
A magnetic field is the lines of force generated by a magnetic. Since a magnetic monopole has never been found, it does not make sense to talk about a magnetic point charge. Instead, lines of magnetic field form closed loops along line of equal magnetic force. The strength of the magnetic field is determined by the number of field lines passing a unit area. The more field lines the stronger the magnetic field. A unit of magnetic field strength is known as the Gauss is defined as one magnetic field line per square centimetre. The direction of the field line could be determined by using a compass needle. Its direction creates a tangent line to the magnetic field at that point.
By convention the arrow tip on magnetic field lines points towards the south magnetic pole and away from the north magnetic pole. The magnetic poles alway occur in pairs, no one has ever found a magnetic monopole, though there is research into their posible existance.
The image shows the field lines produced by a bar magnet. Iron fillings are sprinked on a piece of paper and the bar-magnet is placed under the paper. The iron-fillings line up and show the intensity of the magnetic field.
| Source | Magnitude of B (T) |
|---|---|
| A hair dryer | ~10 -7-10-3 |
| Sunlight | ~ 3 x 10-6 |
| Colour TV | ~ 10-6 |
| A small bar magnet will produce | ~10-2 |
| At a sunspot B | ~ 0.3 |
| MRI body scanner magnet | ~ 2 |
| Reseach Physics Labs produce up to | ~50 |
| The field at the surface of a neutron star | ~108 |
Types of Magnetism
Before discussing the different types of magnetism we need clear up a few definitions which are used to categorise the types of magnetism.
Magnetic Suseptibily
As the magnetic field increases, the magnetic flux increases. We denote magnetic field intensity by H and magnetic flux by B the constant of proportionality is μ0 this is known as the magnetic permitivity
In a vacuum, μ0 has a value of 4π x 10-7 H m-1 in SI units
For other materials this proportionality is expressed with the relative permitivity, μr
The susceptibility χ is defined in terms of the relative permitivity. χ = (μr - 1)
Ferromagnetism

This is when a large proportion of the individual atomic magnetic momements line up and produce a strong magnetic field. Iron a strongly ferromagnet. An external magnetics field can be used to align the atomic magnetic momements. When the external magnetic field is removed the magnetic moments remain in the same direction provided they do not receive a shock or are heated above the Currie temperature where the thermal motion can randomise the magnetic alignment.
Anti Ferromagnetism
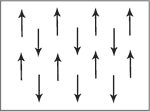
Anti-ferromagnetic materials show patterns of magnetic spin with neighbouring atoms spin arranged in opposite directions. Typically antiferromagnetism is exhibited at low temperatures. As spins cancel each other out, mostly this results in paramagnetic behavior but can also show in ferrimagnetic behavior.
Ferrimagnetism
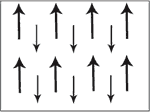
Ferri magentic material have two sets of magnetic dipole moments pointing in opposite directions. The magnetic moments do not cancel each other out becauses the dipole moment in one direction is smaller than the other. On a B-H graph ferrimagnetism is like ferromagnetism.
Paramagnetism

Paramagnetic materials such as liquid oxygen and aluminium show a weak magnetic attraction when placed near a magnet. Some atoms or ions in the material have a net magentic moment due to unpaired electrons in partially filled orbitals. In the presence of a field, there is a partial alignment of the atomic magnetic moments in the direction of the field resulting in a net positive magnetisation and positive susceptibility.
In a strong magnetic field, paramagnetic materials become magentic and will stay magnetic while the field is present. When the strong magnetic field is removed the net magnetic alignment is lost and the magnetic dipoles relax to a random motion.
Diamagnetism

Diamagnetic materials are composed of atoms that have no net magnetic moments. However, when exposed to a field a weak negative magnetisation is produced which causes repulsion instead of attraction. Diamagnetic materials have negative susceptibilty with magnetitude of around -10
Many common materials are diamagnetic and hence In the presence of very strong magentic fields the repulsion caused by diamagnetism can cause objects to levitate even frogs.
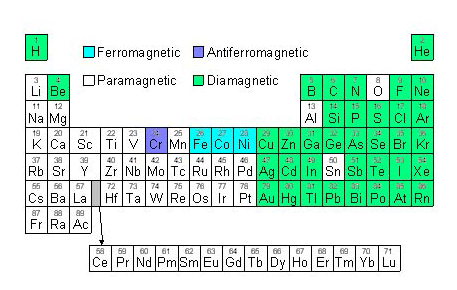
Quantum Theory of Magnetism
All this is very well but it is a bit odd why only a few elements are magnetic but others are not. To explain why requires information about the atomic structure of the elements and how they interact. We need quantum physics to explain.
The magnetic moment consists of two distinct sources. The electron is a particle which has its own spin which can take on values of ± 1/2 ħ. The nucleus also has protons and neutrons which also have their own intrinsic spins, however the magnetic moment is inversely proportional to the mass so in comparison with the electron the magnetic moment of the nucleus is minimal.
The Bohr magneton is the unit given to the electron magnetic dipole moment:
μB = eħ/(2me)
In SI units this μB = 9.274 x 10-24 A m2
There is also a contribution to the magnetic moment produced by the electron moving around the nucleus can be considered to act as a current loop. The magnitude of the magnetic moment is related to the angular momentum of the electron travelling around the nucleus.
We can calculate the contribution to the magnetic moment of the electron. Consider an electron of mas m and charge e orbiting in a fixed, circular orbit a distance R from the centre. The electron is moving with constant velocity v
The angular momentum of the electron, is then
J = R x mev = meR v n^
The current produced by the electron orbiting is given from the definition of current a charge flow per unit time or
I = dQdt = -e/T.
T = 2πR/v = -e v/(2πR)
Where T is the period of the electron orbit.
The magnƒetic moment is μ = IS = -e v/(2πR) πR2n^ = - 1/2 e v R n^
We can rewrite the magnetic moment in terms of J as γJ (if we let γ = - e/(2me))
We call γ the gyromagnetic ratio
If J = mħ, μ = - m(eħ/(2me)) = mμB
Rerefences
- Magnetism Notes - university of Birmingham.
- Magnet Man Cool experiments with magnets
- Cambridge University Department of Engineering
- University of Delaware - magnetism
- Kittel Solid State Physics
- The Solid State - from Superconductors to Superalloys
